“미분”과 “적분”은 수학에서 중요한 개념으로, 함수의 변화를 분석하고 면적을 계산하는 데 사용됩니다.
“미분/적분”을 영어로 표현할 수 있는 방법
- Differentiation (미분)
- Integration (적분)
- Derivative (미분의 결과)
- Integral (적분의 결과)
1. Differentiation
“Differentiation”은 함수의 변화를 분석하여 기울기를 구하는 과정입니다.
- “Differentiation is used to find the rate of change of a function.” (미분은 함수의 변화율을 찾는 데 사용된다.)
- “In calculus, differentiation helps determine the slope of a curve.” (미적분학에서 미분은 곡선의 기울기를 결정하는 데 도움이 된다.)
2. Integration
“Integration”은 함수 아래의 면적을 계산하거나 누적된 값을 찾는 과정입니다.
- “Integration is used to calculate the area under a curve.” (적분은 곡선 아래의 면적을 계산하는 데 사용된다.)
- “In calculus, integration helps find the total accumulated value.” (미적분학에서 적분은 전체 누적 값을 찾는 데 도움이 된다.)
3. Derivative
“Derivative”는 미분의 결과로, 함수의 순간적인 변화율을 나타냅니다.
- “The derivative of a function shows how the function changes with respect to its variable.” (함수의 미분은 함수가 변수에 대해 어떻게 변화하는지를 보여준다.)
- “The slope of the tangent line at any point on a curve is given by the derivative.” (곡선 위의 어떤 지점에서의 접선의 기울기는 미분에 의해 주어진다.)
4. Integral
“Integral”은 적분의 결과로, 함수의 면적 또는 누적된 값을 나타냅니다.
- “The integral of a function represents the area under the curve from a to b.” (함수의 적분은 a에서 b까지 곡선 아래의 면적을 나타낸다.)
- “Finding the integral of a function is crucial for solving many problems in physics and engineering.” (함수의 적분을 찾는 것은 물리학과 공학의 많은 문제를 해결하는 데 중요하다.)
“미분/적분”을 영어로 표현할 때는 “Differentiation,” “Integration,” “Derivative,” 또는 “Integral”과 같은 표현을 사용할 수 있습니다.







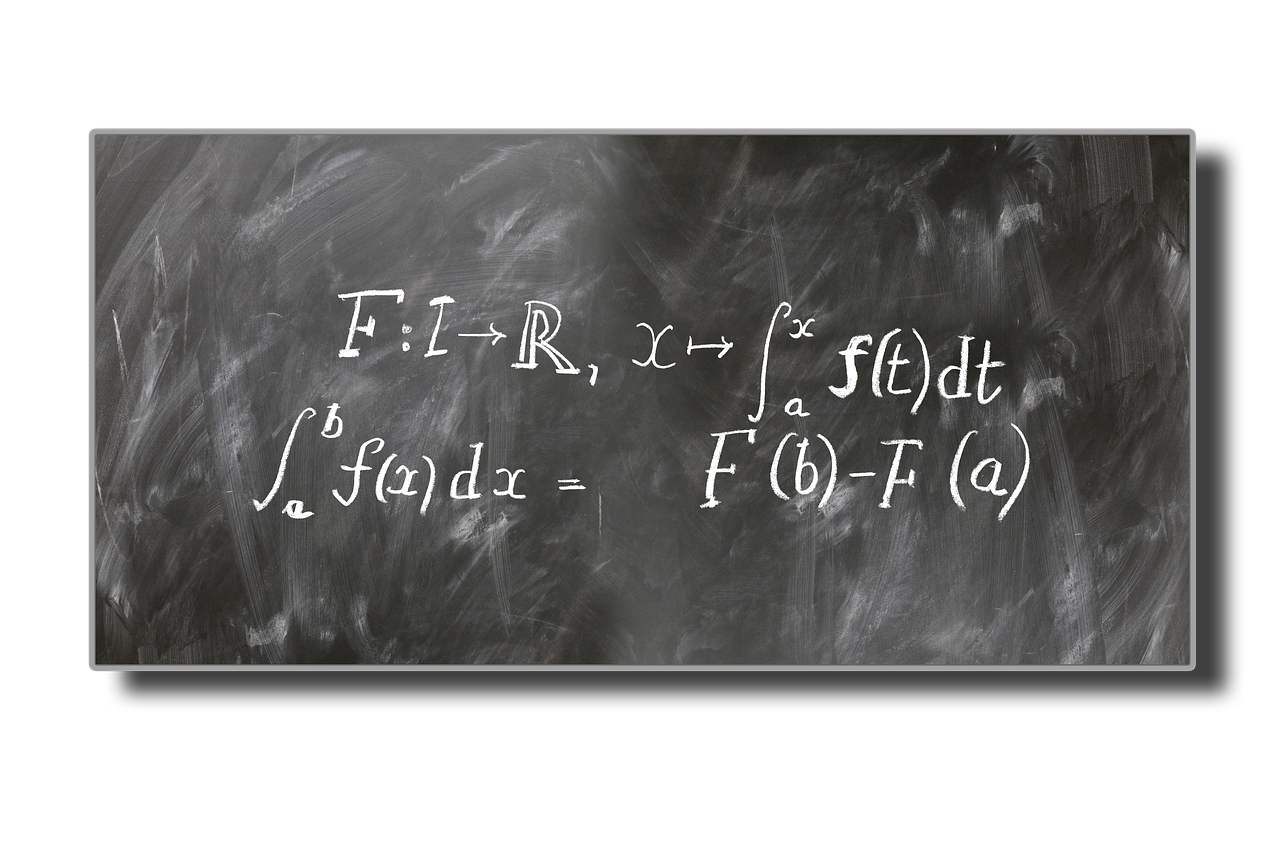





Leave a Reply