“사분면”은 영어로?

“사분면”은 영어로 “quadrant”로 번역됩니다. 이 표현은 주로 좌표평면을 네 개의 영역으로 나누는 개념을 나타냅니다.

1. Quadrant (사분면)

이 표현은 Cartesian 좌표계에서 x축과 y축에 의해 형성되는 네 개의 영역 중 하나를 나타냅니다.

“The Cartesian plane is divided into four quadrants.” (카르테시안 평면은 네 개의 사분면으로 나뉜다.)
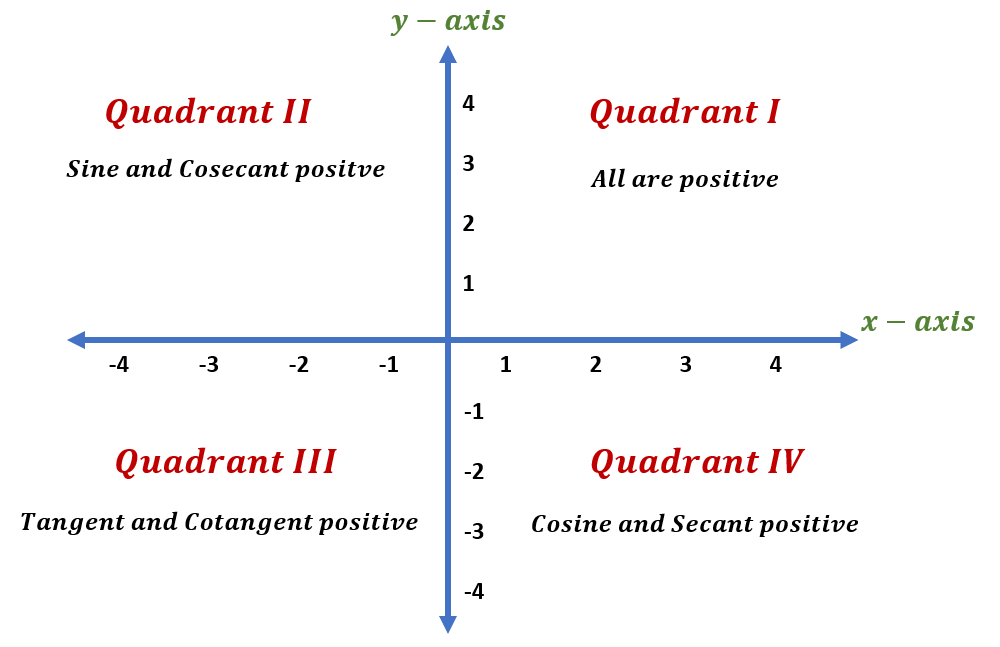
“Each quadrant has specific characteristics based on the signs of x and y coordinates.” (각 사분면은 x와 y 좌표의 부호에 따라 특정한 특성을 가진다.)
“Understanding quadrants is essential for graphing functions.” (사분면을 이해하는 것은 함수 그래프를 그리는 데 필수적이다.)

2. First Quadrant (제1사분면)

이 표현은 x와 y가 모두 양수인 사분면을 지칭합니다.

“In the first quadrant, both x and y values are positive.” (제1사분면에서는 x와 y 값이 모두 양수이다.)
“Many mathematical functions are primarily studied in the first quadrant.” (많은 수학적 함수는 주로 제1사분면에서 연구된다.)
“The first quadrant is where we find the coordinates of most real-world applications.” (제1사분면은 대부분의 실제 응용 프로그램의 좌표가 위치하는 곳이다.)

3. Second Quadrant (제2사분면)

이 표현은 x는 음수이고 y는 양수인 사분면을 나타냅니다.

“In the second quadrant, x values are negative while y values are positive.” (제2사분면에서는 x 값은 음수이고 y 값은 양수이다.)
“Trigonometric functions behave differently in the second quadrant.” (삼각함수는 제2사분면에서 다르게 작용한다.)
“Identifying the second quadrant helps in understanding the overall graph.” (제2사분면을 식별하는 것은 전체 그래프를 이해하는 데 도움을 준다.)

4. Third Quadrant (제3사분면)

이 표현은 x와 y가 모두 음수인 사분면을 설명합니다.

“Both x and y values are negative in the third quadrant.” (제3사분면에서는 x와 y 값이 모두 음수이다.)
“The third quadrant is often associated with certain types of angles in trigonometry.” (제3사분면은 종종 삼각법에서 특정 유형의 각도와 연관된다.)
“Graphing equations can reveal important features in the third quadrant.” (방정식을 그래프로 나타내면 제3사분면의 중요한 특성을 드러낼 수 있다.)

5. Fourth Quadrant (제4사분면)

이 표현은 x는 양수이고 y는 음수인 사분면을 나타냅니다.

“In the fourth quadrant, x values are positive while y values are negative.” (제4사분면에서는 x 값은 양수이고 y 값은 음수이다.)
“Understanding the fourth quadrant is crucial for interpreting certain graphs.” (제4사분면을 이해하는 것은 특정 그래프를 해석하는 데 중요하다.)
“Many real-world scenarios can be represented in the fourth quadrant.” (많은 실제 시나리오는 제4사분면에서 표현될 수 있다.)

“사분면”은 수학과 그래픽에서 중요한 개념으로, 좌표계에서 위치와 관계를 이해하는 데 필수적입니다. 이러한 표현들은 각각의 사분면의 특징을 설명하고, 데이터를 분석하는 데 도움을 줍니다.

Archives